Klasa 7 Ciąg Fibonacciego
CIĄG FINOBACCIEGO
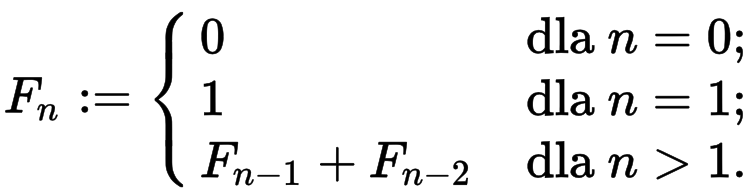
Jego historia sięga 1202 roku, kiedy to Leonard z Pizy, zwany Fibonaccim, przestawił ciąg jako rozwiązanie zadania o rozmnażaniu się królików w swoim dziele Liber abaci. Ciąg przyjął nazwę "ciągu Fibonacciego" dopiero w XIX wieku, za sprawą Édouarda Lucasa.
Z definicji ciąg Fibonacciego to taki ciąg liczbowy, w którym pierwszy wyraz jest równy 0, drugi 1, a każdy kolejny jest sumą dwóch poprzednich. Niektórzy jednak nie wliczają zera do elementów ciągu, jest to kwestia umowna.
Ciąg Fibonacciego - WZÓR
Wzór ogólny ciągu można przedstawić rekurencyjnie. Jest to pierwszy ze znanych ciągów tego rodzaju. Przyjmijmy oznaczenie Fn dla n-tego wyrazu ciągu. Zapis formalny będzie wtedy wyglądał następująco:

Początkowe wartości tego ciągu wynoszą: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... Każdy z wyrazów ciągu Fibonacciego nazywamy liczbą Fibonacciego.
Z ciągiem Fibonacciego jest związane pojęcie liczby złotego podziału. Biorąc każdy kolejny wyraz ciągu (za wyjątkiem pierwszych dwóch wyrazów: zera i jedynki) i dzieląc go przez jego poprzednik otrzymamy iloraz bliski liczbie 1,618. Jest to tak zwana liczba złotego podziału. Im dalszy wyraz ciągu, tym odchylenie od tej wartości jest mniejsze. Przy n dążącym do nieskończoności granica ciągu wynosi dokładnie:

Choć na dzień dzisiejszy nikt już chyba nie oblicza ręcznie tych wartości, gdyż są one doskonale znane to jako ciekawostkę warto wskazać jak obliczamy taki ciąg. Jest to nic innego jak ciąg liczb naturalnych określony w następujący sposób:
Pierwszy wyraz jest równy 0, drugi jest równy 1, każdy kolejny jest sumą dwóch poprzednich.
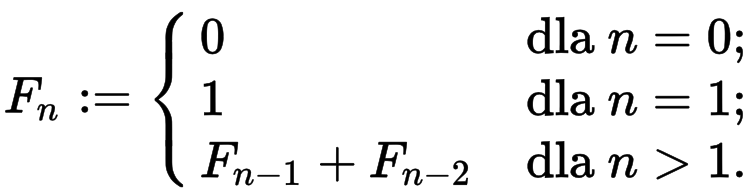
Pierwsze wyrazy ciągu uzyskuje się zatem poprzez zsumowanie dwóch poprzednich:
0 + 1 = 11 + 1 = 21 + 2 = 32 + 3 = 53 + 5 = 85 + 8 = 138 + 13 = 2113 + 21 = 3421 + 34 = 5534 + 55 = 89
Ciąg Fibonacciego: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Zadanie - sprawdźcie czy to co jest napisane poniżej jest prawdą:
Ciąg Fibonacciego - co to takiego?
Jego historia sięga 1202 roku, kiedy to Leonard z Pizy, zwany Fibonaccim, przestawił ciąg jako rozwiązanie zadania o rozmnażaniu się królików w swoim dziele Liber abaci. Ciąg przyjął nazwę "ciągu Fibonacciego" dopiero w XIX wieku, za sprawą Édouarda Lucasa.
Z definicji ciąg Fibonacciego to taki ciąg liczbowy, w którym pierwszy wyraz jest równy 0, drugi 1, a każdy kolejny jest sumą dwóch poprzednich. Niektórzy jednak nie wliczają zera do elementów ciągu, jest to kwestia umowna.
Ciąg Fibonacciego - WZÓR
Wzór ogólny ciągu można przedstawić rekurencyjnie. Jest to pierwszy ze znanych ciągów tego rodzaju. Przyjmijmy oznaczenie Fn dla n-tego wyrazu ciągu. Zapis formalny będzie wtedy wyglądał następująco:

Początkowe wartości tego ciągu wynoszą: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... Każdy z wyrazów ciągu Fibonacciego nazywamy liczbą Fibonacciego.
Z ciągiem Fibonacciego jest związane pojęcie liczby złotego podziału. Biorąc każdy kolejny wyraz ciągu (za wyjątkiem pierwszych dwóch wyrazów: zera i jedynki) i dzieląc go przez jego poprzednik otrzymamy iloraz bliski liczbie 1,618. Jest to tak zwana liczba złotego podziału. Im dalszy wyraz ciągu, tym odchylenie od tej wartości jest mniejsze. Przy n dążącym do nieskończoności granica ciągu wynosi dokładnie:

Odpowiedź proszę napisać jako wiadomość do mnie przez Librusa.
zadanie na szóstkę - proszę zrobić w Scratch program liczący ciąg Finobacciego
Tutaj możesz zobaczyć jak taki program wygląda: KLIKNIJ TUTAJ
ZADANIE ZAMIENNE
Proszę KLIKNĄĆ TUTAJ
wybrać 2 przykłady, przeczytać i pisemnie uzasadnić dlaczego wybrałaś/łeś taki przykład.
Pracę proszę przesłać przez DE Liburs.

Komentarze
Prześlij komentarz